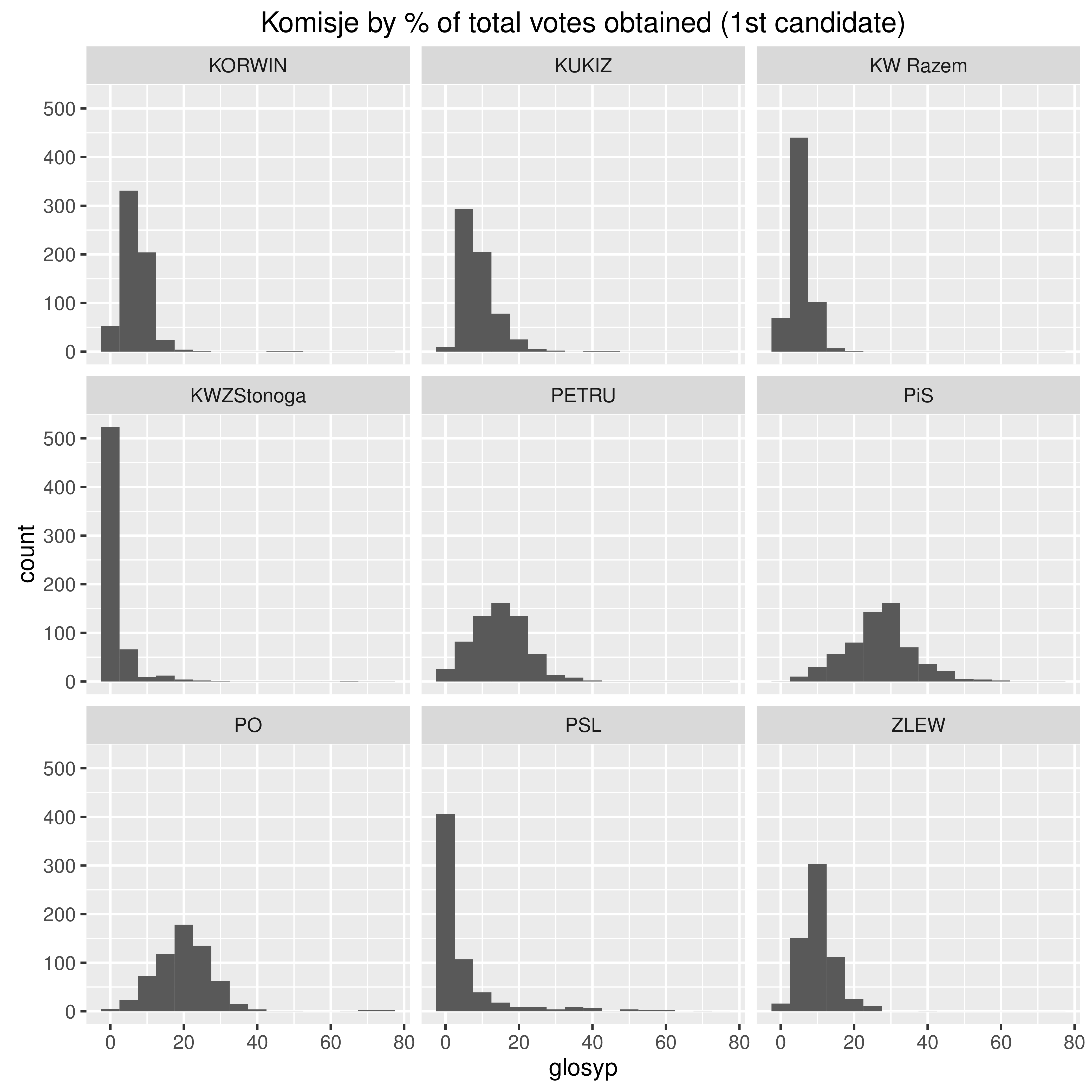
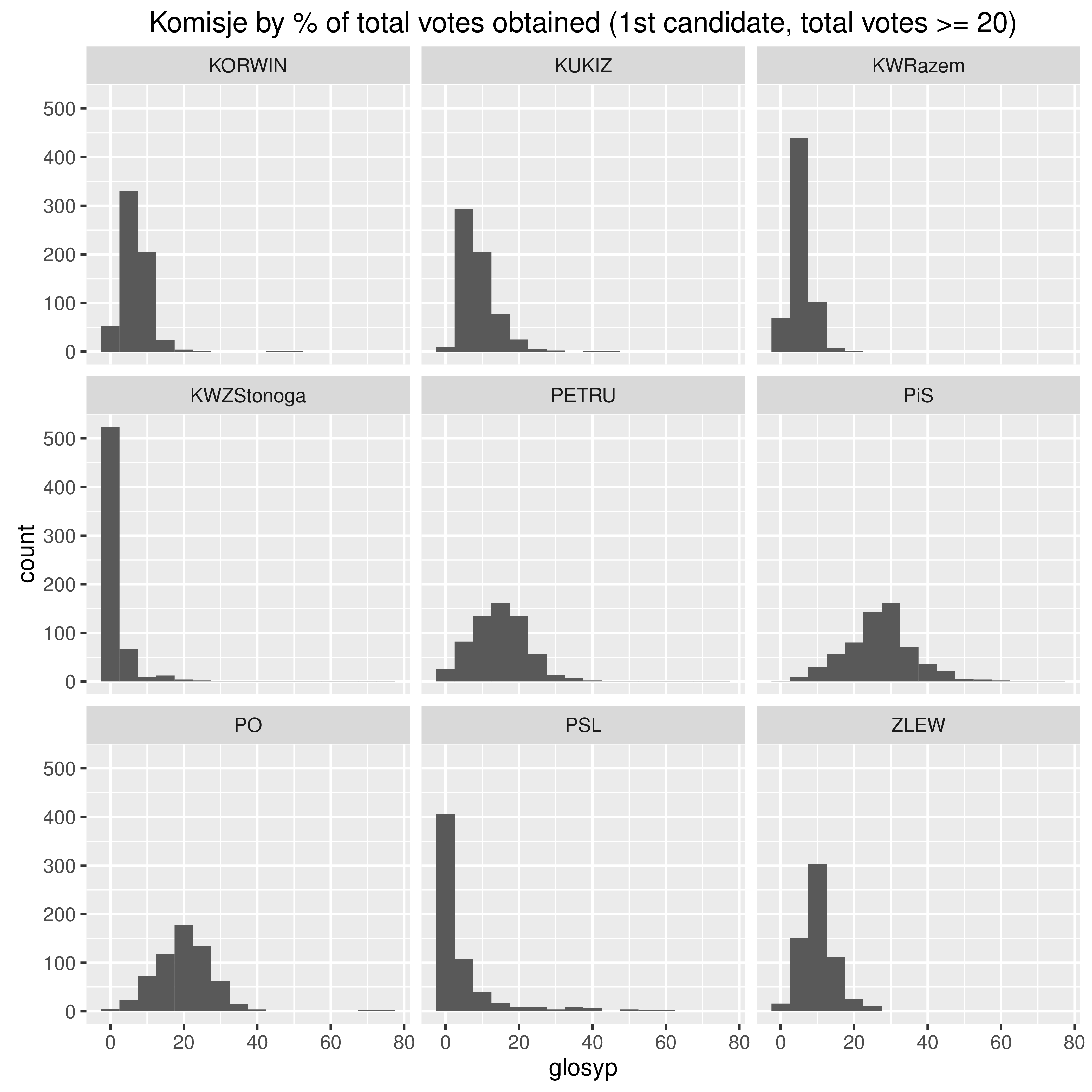
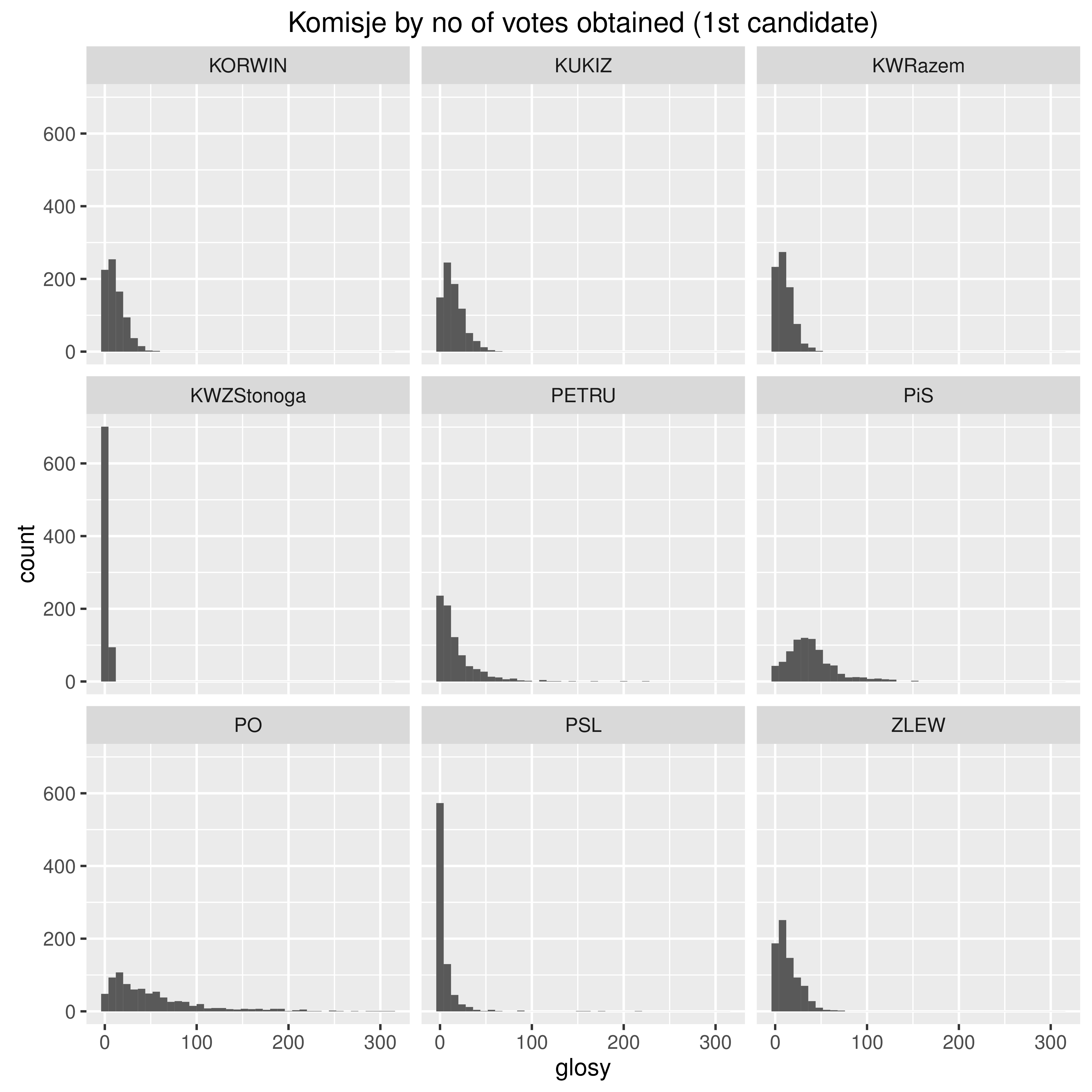
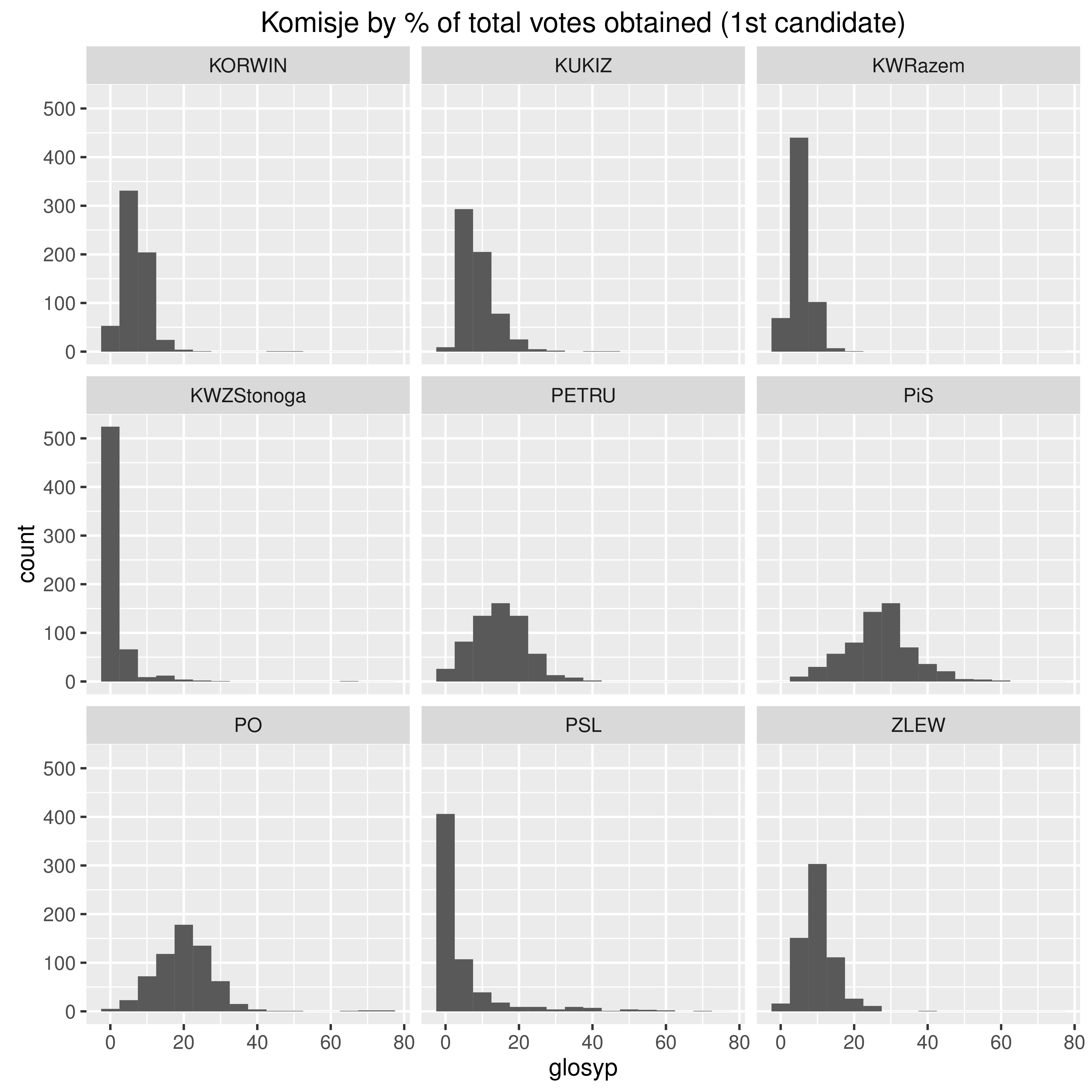
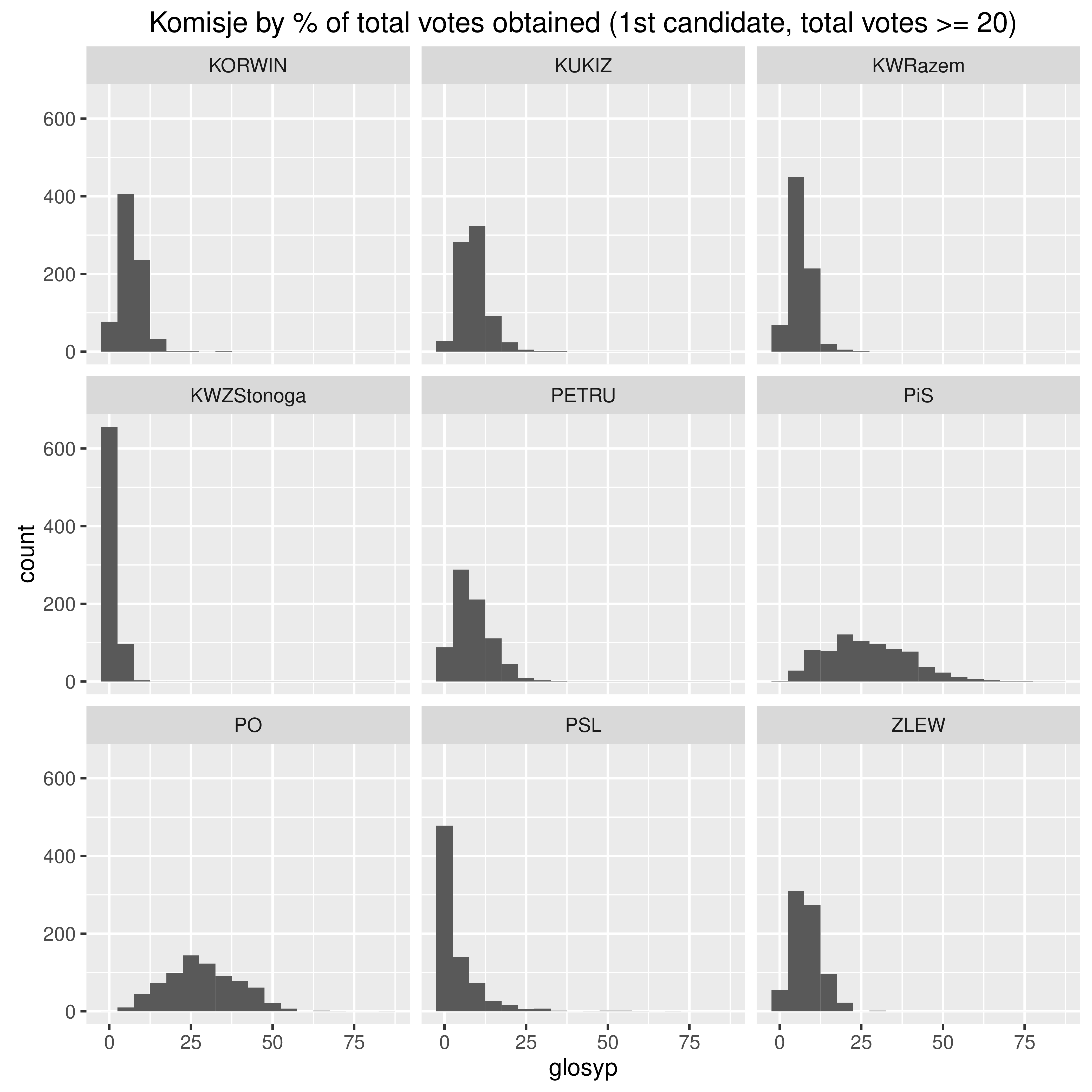
Uczono mnie, że współczynnik skośności aczkolwiek może przyjąć wartości większe od 3, to w praktyce taka sytuacja się nie zdarza. Dlatego z rezerwą podszedłem do obliczeń, z których wynikało, że dla pewnego zbioru danych wynosi on 14:
library(moments)
# Wynik 1-ki z listy komitetu Z.Stonogi (D.Hojarska, wybory 2015)
s <- read.csv("hojarska.csv", sep = ';', header=T, na.string="NA");
skewness(s$glosy)
[1] 14.08602
nrow(s)
[1] 657
sum(s$glosy)
[1] 1671
Pierwsza hipoteza jest taka, że formuła liczenia współczynnika może być egzotyczna. Ustalmy zatem jak toto jest liczone:
?skewness
Description:
This function computes skewness of given data
Wiele to się nie dowiedziałem. Po ściągnięciu źródła można ustalić, że to współczynnik klasyczny czyli iloraz trzeciego momentu centralnego przez odchylenie standardowe do trzeciej potęgi. Zatem jak najbardziej klasyczny a nie egzotyczny. Sprawdźmy co wyliczy Perl dla pewności:
#!/usr/bin/perl
print STDERR "** Użycie: $0 plik numer-kolumny (pierwszy wiersz jest pomijany)\n";
print STDERR "** Domyślnie: wyniki kandydata nr1 na liście komitetu Z.Stonoga (okr.25 / D.Hojarska)\n";
$file = "hojarska.csv"; ## default file
$column = 1; ## first column = 0
if ( $#ARGV >= 0 ) { $file=$ARGV[0]; }
if ( $#ARGV >= 1 ) { $column=$ARGV[1]; }
open (S, "$file") || die "Cannot open $file\n";
print "\nDane z pliku $file (kolumna: $column):\n";
$hdr = <S> ; # wczytaj i pomin naglowek ($n będzie prawidłowe)
while (<S>) { chomp();
@tmp = split (/;/, $_);
$v = $tmp[$column];
push(@L, $v) ;
$sum += $v;
$Counts{"$v"}++;
$n++;
}
# Wyznaczenie średniej:
$mean = $sum /$n;
## Wyznaczenie dominanty:
## przy okazji wydrukowanie danych pogrupowanych
print "+--------+---------+--------+--------+--------+\n";
print "| Głosy | Obwody | cumGł | cumGł% | cumN% |\n";
print "+--------+---------+--------+--------+--------+\n";
$maxc = -1;
for $c (sort {$a <=> $b } keys %Counts ) {
$sumCum += $Counts{"$c"} * $c;
$nCum += $Counts{"$c"};
if ($maxc_pos < $Counts{$c} ) {
$maxc_pos = $Counts{$c} ; $maxc_val = $c
}
printf "| %6d | %6d | %6d | %6.2f | %6.2f |\n",
$c, $Counts{$c}, $sumCum, $sumCum/$sum *100, $nCum/$n *100;
}
print "+--------+---------+--------+--------+--------+\n\n";
$mode = $maxc_val; # dominanta
## Wyznaczenie mediany:
$half = int(($#L +1)/2 );
@L = sort ({ $a <=> $b } @L) ; #numerycznie
##print "$half of @L\n";
$median = $L[$half];
printf "Średnie: x̄ = %.3f (N=%d) Me =%.3f D = %.3f\n", $mean, $n, $median, $mode;
## Odchylenia od średniej:
for my $l (@L) {##
$sd1 = ($l - $mean) ;
$sd2 = $sd1 * $sd1; # ^2
$sd3 = $sd2 * $sd1; # ^3
$sum_sd1 += $sd1; $sum_sd2 += $sd2;
$sum_sd3 += $sd3;
}
# odchylenie std./3-ci moment:
$sd = sqrt(($sum_sd2 / $n));
$u3 = $sum_sd3/$n;
printf "Sumy (x-x̄): %.2f(¹) %.2f(²) %.2f(³)\n",
$sum_sd1, $sum_sd2, $sum_sd3;
printf "Rozproszenie: σ = %.3f µ³ = %.3f\n", $sd, $u3;
printf "Skośność: (x̄-D)/σ = %.2f", ($mean -$mode)/$sd;
printf " 3(x̄-Me)/σ) = %.2f", 3 * ($mean - $median)/$sd;
printf " (µ³/σ³) = %.2f\n", $u3/($sd*$sd*$sd);
##//
Uruchomienie powyższego skryptu daje w wyniku to samo. Moja pewność, że wszystko jest OK jest teraz (prawie że) stuprocentowa.
Wracając do R:
library(ggplot2);
p <- ggplot(data = s, aes(x = glosy)) + geom_histogram(binwidth = 4)
p
breaks <- ggplot_build(p)$data
breaks
[[1]]
y count x xmin xmax density ncount ndensity PANEL group
1 482 482 0 -2 2 0.1834094368 1.000000000 2628.000000 1 -1
2 140 140 4 2 6 0.0532724505 0.290456432 763.319502 1 -1
...
Pierwszy przedział jest definiowany jako (-2;2], ale z uwagi na wartość danych de facto liczy głosy w komisjach, w których Hojarska dostała 0--2 głosów (drugi to (2;6], itd) i ni cholery nie da się tego zmienić na coś bardziej zbliżonego do prawdy. Bo tak jak jest to faktycznie pierwszy przedział jest dwa razy węższy niż każdy pozostały. W szczególności prawdziwa średnia, w tym przedziale wynosi 1,259 głosa, zaś liczona jako środek przedziału przez liczebność wynosi 1.0 (482 *1/482). Wg formuły ggplota środek przedziału to zero zatem średnia też wyjdzie 0, tj. wartość jest wyznaczona z dużym/nieokreślonym błędem.
Dzieje się tak ponieważ: the histogram is centered at 0, and the first bars xlimits are at 0.5*binwidth and -0.5*binwidth. Dopiero gdy dane są dodatnie, to ggplot zaczyna od zera. No ale nasz zbiór zawiera zera i klops. Zmiana tego jest nietrywialna.
Zamiast ggplota moża użyć po prostu polecenia hist:
h <- hist(s$glosy, breaks=seq(0,max(s$glosy), by=4) )
h
$breaks
[1] 0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72
[20] 76 80 84 88 92 96 100 104 108 112 116 120 124 128 132 136 140 144 148
[39] 152
$counts
[1] 592 42 6 4 2 2 2 1 2 1 2 0 0 0 0 0 0 0 0
[20] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
$density
[1] 0.2252663623 0.0159817352 0.0022831050 0.0015220700 0.0007610350
[6] 0.0007610350 0.0007610350 0.0003805175 0.0007610350 0.0003805175
[11] 0.0007610350 0.0000000000 0.0000000000 0.0000000000 0.0000000000
[16] 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
[21] 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
[26] 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
[31] 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
[36] 0.0000000000 0.0000000000 0.0003805175
$mids
[1] 2 6 10 14 18 22 26 30 34 38 42 46 50 54 58 62 66 70 74
[20] 78 82 86 90 94 98 102 106 110 114 118 122 126 130 134 138 142 146 150
No teraz liczy (prawie) jak trzeba pierwszy przedział [0;4], drugi (4;8] itd. Prawie bo na upartego pierwszy przedział jest szeroki na 5 wartości a kolejne na 4. Eh te detale i te upierdliwe zero:-)
Przy okazji się zadumałem, a cóż to jest to density. W pierwszym podejściu, że to są częstości, ale nie, bo ewidentnie nie sumują się do 1:
?hist
density: values f^(x[i]), as estimated density values. If
`all(diff(breaks) == 1)', they are the relative frequencies
`counts/n' and in general satisfy sum[i; f^(x[i])
(b[i+1]-b[i])] = 1, where b[i] = `breaks[i]
No dość kryptycznie, ale można się domyśleć, że nie $\sum_i d_i =1$, ale $\sum_i d_i * w_i$, gdzie $w_i$, to szerokość przedziału $i$ (a $d_i$ oznacza gęstość w przedziale $i$ oczywiście). Pole pod krzywą będzie zatem równe 1, jak tego należy się spodziewać po gęstości.
Wprawdzie już to padło mimochodem wyżej, ale analizowany zbiór danych to liczba oddanych głosów na numer jeden na liście komitetu wyborczego Zbigniewa Stonogi w okręgu wyborczym 25 w wyborach do Sejmu w 2015 roku. Tym numerem jeden była Danuta Hojarska, która faktycznie dostała 152 głosy w jednej komisji (we wsi, w której mieszka) oraz 0--4 głosów w 90% pozostałych komisjach (w tym 0 głosów w 191/657.0 = 29% komisjach).
Analiza przestrzenna
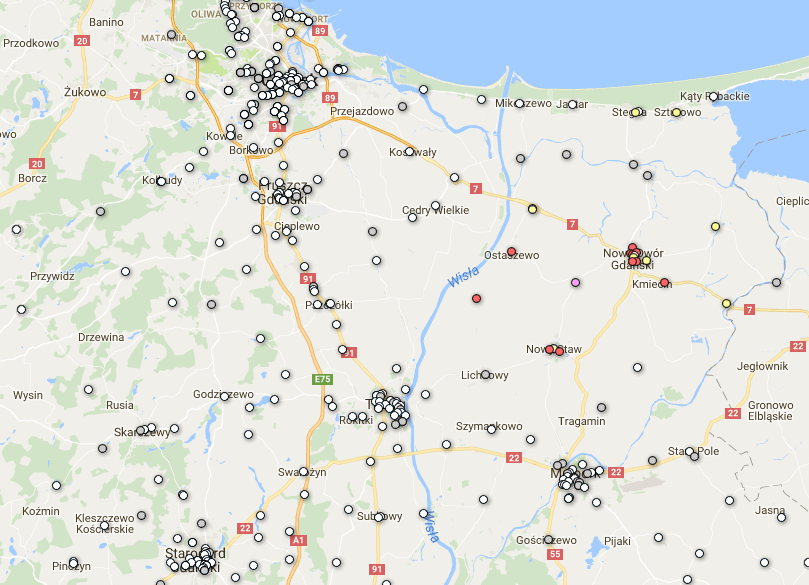
Ze starych zapasów odgrzebałem plik CSV ze współrzędnymi obwodowych komisji wyborczych i połączyłem go z wynikami uzyskanymi przez Hojarską z zamiarem wyświetlenia tego na mapie za pomocą Google Fusion Tables (GFT):
obwod;coordexact;glosy;icon
101884;54.2701205 18.6317438;3;measle_white
101885;54.260714 18.6282809;0;measle_white
101886;54.262187 18.632082;2;measle_white
101887;54.257501 18.63147;1;measle_white
101888;54.25786 18.6306574;7;measle_grey
...
Kolumna icon zawiera nazwę ikony, która jest definiowana wg schematu: 0--3 głosy biala (measle_white); 4--9 głosów szara (measle_grey) 9-19 głosów żółta (small_yellow) 20--99 głosów czerwona (small_red) 100 i więcej głosów purpurowa (small_purple). Zestawienie dostępnych w GFT ikon można znaleźć tutaj. Konfigurowanie GFT aby korzystała z kolumny z nazwami ikon sprowadza się do wyklikania stosownej pozycji (Configure map →Feature map →Change feature styles →Use icon specified in a column.)
Przy okazji odkurzyłem zasób skryptów/zasobów używanych do geokodowania i/lub przygotowywania danych pod potrzeby GFT, w szczególności: joincvs.pl (łączy dwa pliki csv w oparciu o wartości n-tej kolumny w pierwszym pliku oraz m-tej kolumny w drugim); geocodeCoder0.pl (uruchamia geokodera Google). Oba skrypty i jeszcze parę rzeczy można znaleźć: tutaj.