Żuławy w koło 2016

Żuławy w koło to maraton rowerowy (czyli przejazd rowerem na dłuższym dystansie -- nie mylić z wyścigiem) organizowany od paru lat na Żuławach jak nazwa wskazuje. Sprawdziłem jak ta impreza wyglądała pod kątem prędkości w roku 2016. W tym celu ze strony Wyniki żUŁAWY wKOŁO 2016 ściągnąłem stosowny plik PDF z danymi, który następnie skonwertowałem do pliku w formacie XLS (Excel) wykorzystując konwerter on-line tajemniczej firmy convertio.pl. Tajemniczej w tym sensie, że nie znalazłem informacji kto i po co tą usługę świadczy.

Konwersja (do formatu CSV) -- jak to zwykle konwersja -- nie poszła na 100% poprawnie i wymagała jeszcze circa 30 minutowej ręcznej obróbki. Być może zresztą są lepsze konwertery, ale problem był z gatunku banalnych i wolałem stracić 30 minut na poprawianiu wyników konwersji niż 2 godziny na ustalaniu, który z konwerterów on-line konwertuje ten konkretny plik PDF (w miarę) bezbłędnie.

Po konwersji wypadało by sprawdzić (chociaż zgrubnie) czy wszystko jest OK.

## Czy każdy wiersz zawieraja 9 pól (powinien)
$ awk -F ';' 'NF != 9 {print NR, NF}' wyniki_zulawy_2016S.csv

## Ilu było uczestników na dystansie 140km?
$ awk -F ';' '$7 ==140 {print $0}' wyniki_zulawy_2016S.csv | wc -l
133

## Ilu było wszystkich (winno być 567 + 1 nagłówek)
$ cat wyniki_zulawy_2016S.csv | wc -l
568 # ok!

Przykładowy wykres pudełkowy

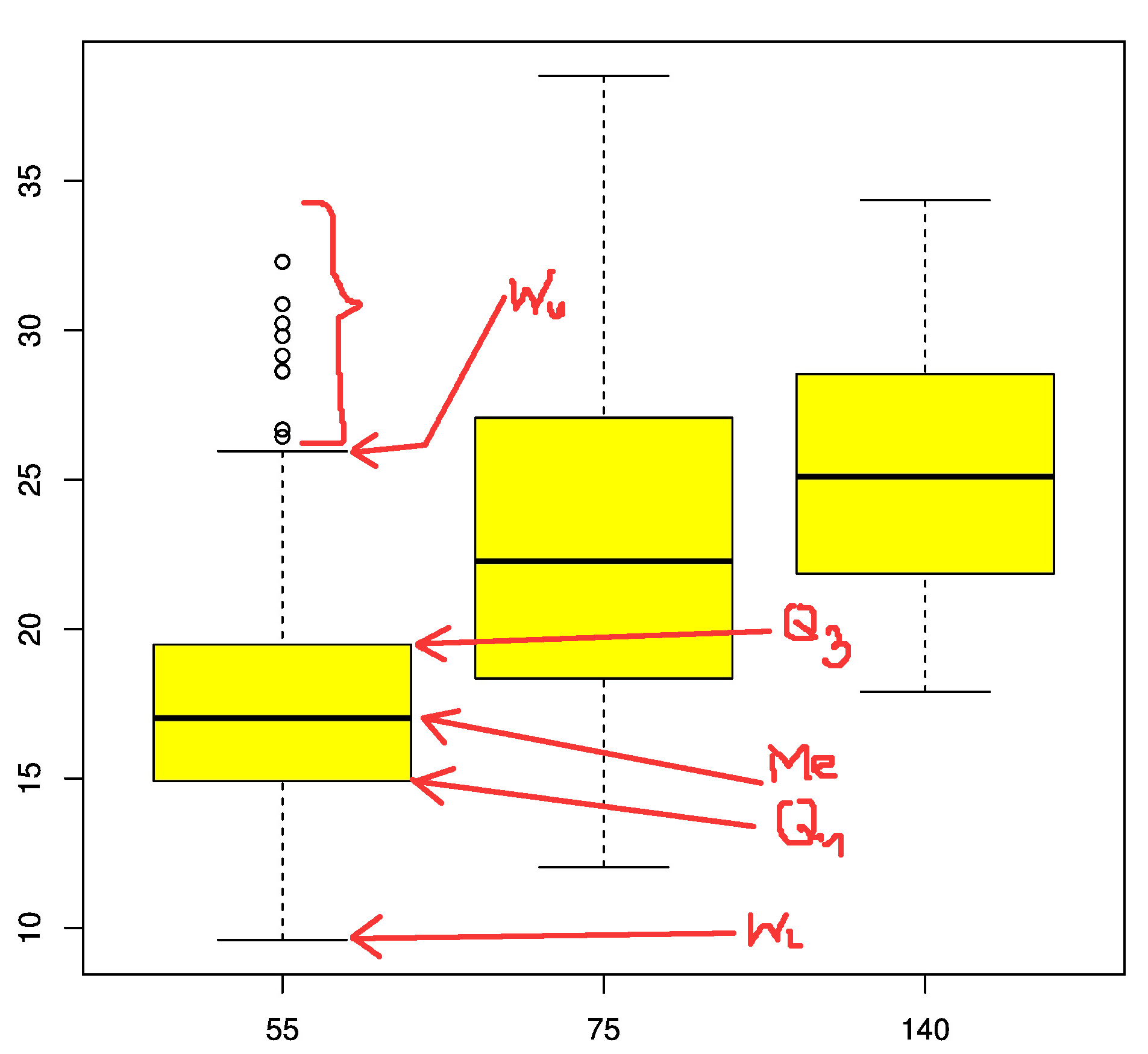
Do analizy statystycznej wykorzystano wykres pudełkowy (porównanie wyników na różnych dystansach) oraz histogram (rozkład średnich prędkości na dystansie 140km). BTW gdyby ktoś nie wiedział co to jest wykres pudełkowy to wyjaśnienie jest na rysunku obok. Objaśnienie: Me, $Q_1$, $Q_3$ to odpowiednio mediana i kwartyle. Dolna/górna krawędź prostokąta wyznacza zatem rozstęp kwartylny (IQR). Wąsy ($W_L$/$W_U$)są wyznaczane jako 150% wartości rozstępu kwartylnego. Wartości leżące poza ,,wąsami'' (nietypowe) są oznaczane kółkami.

Ww. wykresy wygenerowano następującym skryptem:

#
co <- "Żuławy wKoło 2016"
#
z <- read.csv("wyniki_zulawy_2016_C.csv", sep = ';',
  header=T, na.string="NA", dec=",");

aggregate (z$meanv, list(Numer = z$dist), fivenum)

boxplot (meanv ~ dist, z, xlab = "Dystans [km]",
    ylab = "Śr.prędkość [kmh]", col = "yellow", main=co )

## tylko dystans 140
z140 <- subset (z, ( dist == 140 ));

## statystyki zbiorcze
s140 <- summary(z140$meanv)
names(s140)

summary_label <- paste (sep='', "Średnia = ", s140[["Mean"]], 
  "\nMediana = ", s140[["Median"]],
  "\nQ1 = ", s140[["1st Qu."]],  "\nQ3 = ", s140[["3rd Qu."]],
  "\n\nMax = ", s140[["Max."]] )
# drukuje wartości kolumny meanv
# z140$meanv
# drukuje wartości statystyk zbiorczych
s140

# wykres słupkowy
h <- hist(z140$meanv, breaks=c(14,18,22,26,30,34,38), freq=TRUE, 
   col="orange", 
   main=paste (co, "[140km]"), # tytuł
   xlab="Prędkość [kmh]",ylab="L.kolarzy", labels=T, xaxt='n' )
# xaxt usuwa domyślną oś 
# axis definiuje lepiej oś OX
axis(side=1, at=c(14,18,22,26,30,34,38))
text(38, 37, summary_label, cex = .8, adj=c(1,1) )

Dane i wyniki są tutaj