Że się zbliżają wybory samorządowe, to ja znowu pochyliłem się nad wynikami z poprzednich tj. z roku 2014. Piszę znowu, bo dane pobrałem dawno temu ze strony http://wybory2014.pkw.gov.pl/. Przypomnę też, że wybory te zakończyły się nielichym skandalem. Po pierwsze system informatyczny Państwowej Komisji Wyborczej zawiódł spektakularnie. Po drugie, nie tylko tradycyjnie odnotowano niską frekwencję, ale dodatkowo i z niewiadomych do końca powodów, doszła niesłychanie wysoka liczba oddanych głosów nieważnych. Po trzecie dramatyczna różnica pomiędzy wynikiem prognozy exit pool, a wynikiem oficjalnym spowodowała, że ówczesna opozycja oskarżyła ówczesnych rządzących o fałszerstwo wyborcze. Różnica sama w sobie nie jest oczywiście czymś niemożliwym, ale też prognozy exit pool są no raczej na tyle dokładne, że na ich podstawie jedni uznają się za wygranych, a inni za przegranych w tzw. cywilizowanym świecie. A w PL akurat ktoś się rąbnął o 50%.
BTW wyobraźmy sobie reakcję #SektyPancernejKonsytytucji (aka #OpozycjiTotalnej) na coś takiego dziś.
Wracając do bazy protokołów. Jest ona niekompletna, co było stanem na czas po wyborach kiedy była pobierana i co (według mnie) było spowodowane przez system informatyczny PKW (czytaj chaos w PKW). Teraz widzę, że baza na stronie PKW wygląda inaczej i być może jest kompletna, ale nie chce mi się tego (na razie) jeszcze raz pobierać. Moja baza jest oryginalna, a nie picowana (żart :-)), a zawiera ponad 96% tego co powinna zawierać (zakładając, że obwodów jest 27435 ja mam 26495). Ta baza jest dostępna tutaj.
Mówiąc konkretnie i porównując z listą 27435 obwodów braki są następujące: Dolnośląskie = 38; Kujawsko-Pomorskie = 17; Lubelskie = 14; Lubuskie = 12; Łódzkie = 14; Małopolskie = 22; Mazowieckie = 1139; Opolskie = 7; Podkarpackie = 10; Podlaskie = 5; Pomorskie = 20; Śląskie = 28; Świętokrzyskie = 13; Warmińsko-Mazurskie = 12; Wielkopolskie = 14; Zachodniopomorskie = 18. Zatem baza jest w miarę kompletna (za wyjątkiem woj. Mazowieckiego, w przypadku którego protokoły nie były opublikowane nawet kilka miesięcy po wyborach).
Każdy protokół zawiera adres i kod teryt komisji obwodowej, tyle że TERYT jest 6 cyfrowy, a nie pełny. Z tego powodu klasyfikację miasto/wieś dokonałem w taki sposób że gmina jest `miejska' jeżeli wg klasyfikacji teryt ma ona typ `gmina miejska' (U) a w każdym innym przypadku (miejsko-wiejska, wiejska, miasto w gminie miejsko-wiejskiej albo obszar wiejski w gminie miejsko-wiejskiej) gmina jest `wiejska' (R). Jest 9996 gmin typu U, a 16881 gmin jest typu R.
Na początek wykonałem prostą analizę eksploracyjną licząc wartości średnie, korelacje oraz regresje pomiędzy głosami nieważnymi a poparciem dla partii. Stosowny fragment R-skryptu wygląda następująco:
## Korelacje pomiędzy % głosów a % głosów niewaznych
cor(d$pgnw14, d$pslp, use = "complete")
## Wykresy rozrzutu ## ###
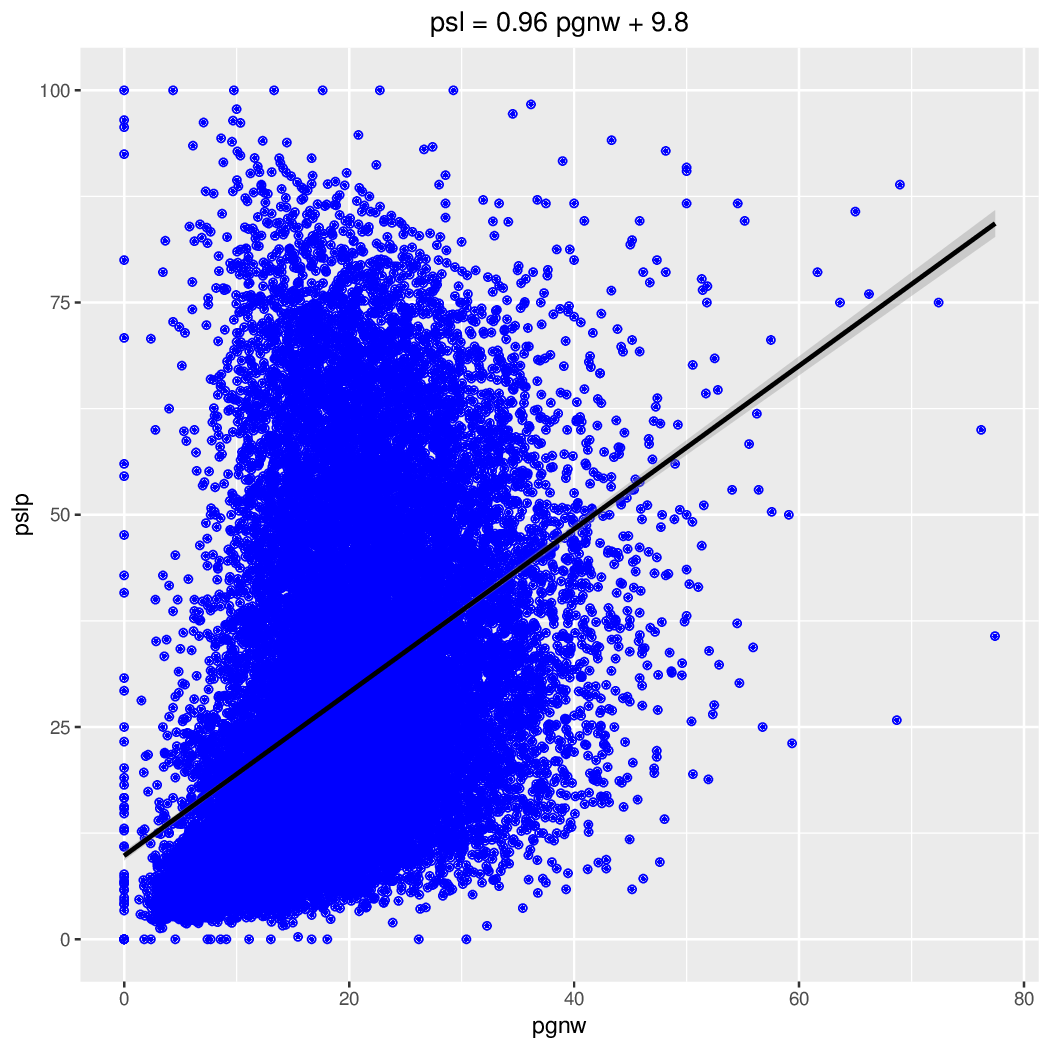
lm <- lm(data=d, pslp ~ pgnw14 ); summary(lm)
lmc <- coef(lm);
title <- sprintf ("psl = %.2f pgnw + %.1f", lmc[2], lmc[1] );
ggplot(d, aes(x = pgnw14, y=pslp )) +
geom_point(colour = 'blue') +
ggtitle(title) +
theme(plot.title = element_text(hjust = 0.5)) +
xlab(label="pgnw") +
ylab(label="pslp") +
geom_smooth(method = "lm", colour = 'black')
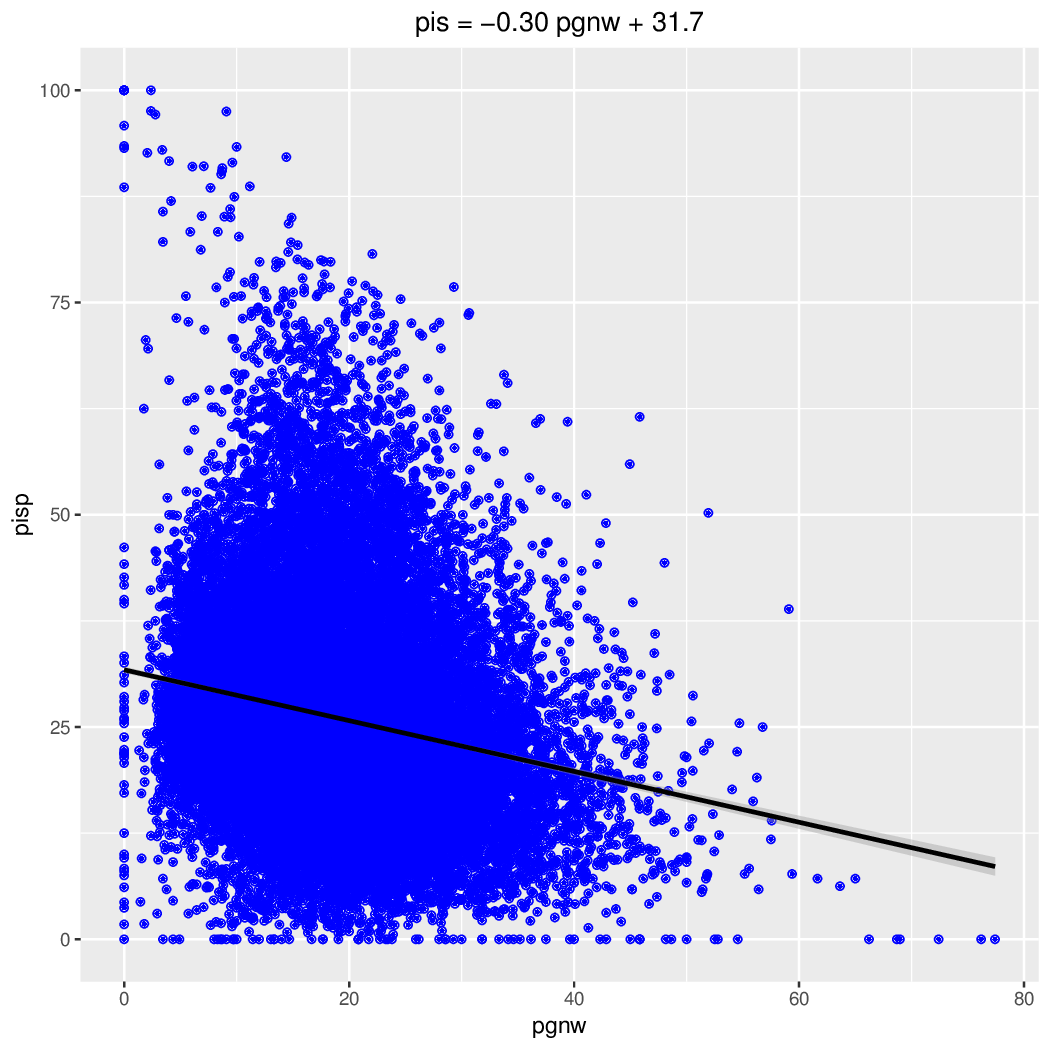
lm <- lm(data=d, pisp ~ pgnw14 ); summary(lm)
Wynik są następujące:
## pgnw (procent głosów nieważnych) Min. 1st Qu. Median Mean 3rd Qu. Max. Grupa 0.00 8.20 11.67 12.82 16.05 56.41 Razem 0.00 12.55 18.18 18.75 23.98 100.00 Miasto 0.00 17.05 21.37 22.15 26.38 77.42 Wieś ## poparcie ## Miasto 0.00 6.719 10.12 13.82 16.53 100.00 PSL 0.00 20.83 25.91 27.12 32.35 100.00 PiS 0.00 25.20 32.56 32.90 39.84 85.00 PO ## Wieś 0.00 20.11 32.61 35.86 49.27 100.00 PSL 0.00 15.42 22.60 25.55 32.96 100.00 PiS 0.00 7.748 15.43 18.53 26.44 92.65 PO ## wsp. korelacji (pgnw vs poparcie) ## PSL PiS PO Grupa 0.4053339 -0.1972364 -0.3321558 Razem 0.4333851 -0.2104114 -0.2648886 Miasto 0.0905243 -0.1931745 -0.0370197 Wieś
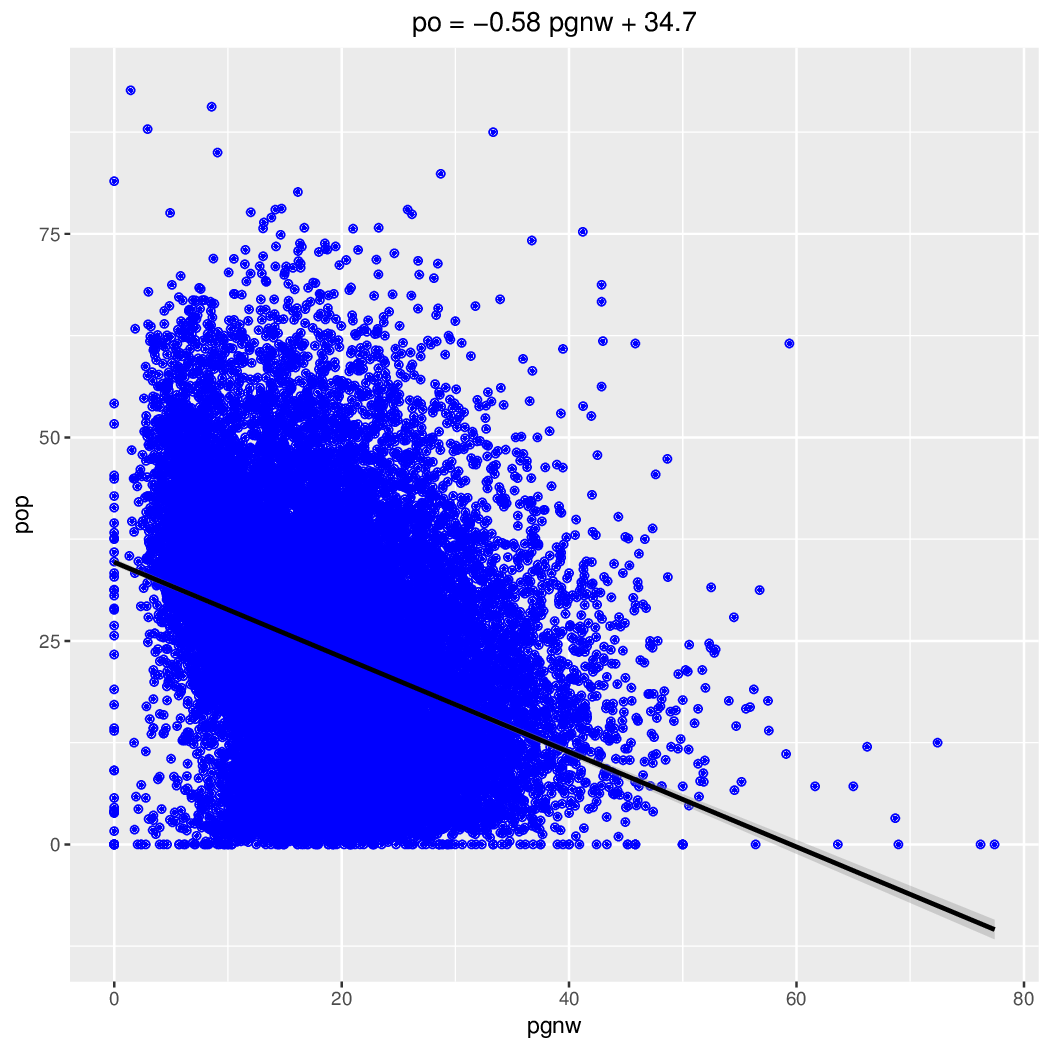
Liczba głosów nieważnych była wyższa na obszarach wiejskich (średnia 22,15% vs 18,75%). Poparcie dla czołowych partii był na wsi najwyższe dla PSL, potem PiS a na końcu PO; w mieście dokładnie odwrotnie. Wystąpiła dodatnia korelacja pomiędzy liczbą głosów nieważnych, a poparciem w przypadku PSL. Nieoczekiwanie była większa na obszarach większych miast, a mniejsza poza nimi. W przypadku zarówno PiS jak i PO korelacja była ujemna (większy udział głosów nieważnych oznacza mniejsze poparcie). Zależność pomiędzy liczbą głosów nieważnych a poparciem ilustrują także wykresy.
Jest zatem różnica między `miastem' a `wsią'. A czy jest różnica w decyzjach w aspekcie przestrzennym? Obliczyłem średnią wartość współczynnika korelacji pomiędzy liczbą głosów nieważnych, a poparciem w powiatach:
powiat <- substr(d$teryt, 0, 4) d[,"powiat"] <- powiat; p.psl <- d %>% group_by(powiat) %>% summarise(V1=cor(pgnw14,pslp)) p.pis <- d %>% group_by(powiat) %>% summarise(V1=cor(pgnw14,pis)) p.po <- d %>% group_by(powiat) %>% summarise(V1=cor(pgnw14,po)) print(p.psl, n=Inf) print(p.pis, n=Inf) print(p.po, n=Inf) > fivenum(p.psl$V1) [1] -0.5984602 0.1066262 0.2906827 0.4491453 0.8536293 > fivenum(p.pis$V1) [1] -0.7985236 -0.4216242 -0.2965959 -0.1658306 0.1877184 > fivenum(p.po$V1) [1] -0.8092580 -0.4891280 -0.3725242 -0.2420753 0.4726305
Jak widać są znaczące różnice...
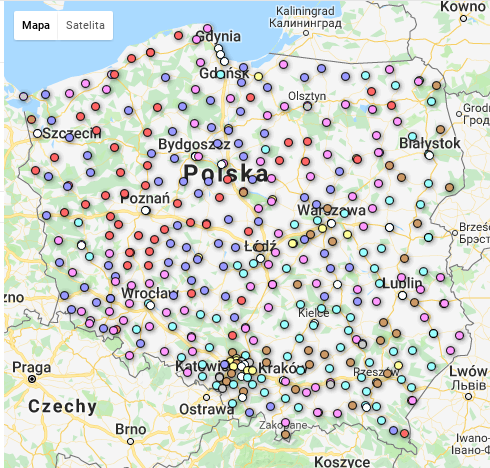
Google Fusion Tables (GFT)
Jedyne narzędzie jakie znam/mam/używam do przestrzennej wizualizacji danych.
Protokoły komisji zawierają adresy. Wykonałem geokodowanie tychże adresów za pomocą geocodera Google. Z różnym skutkiem, mianowicie 27435 komisji zgeokodowało się na 21716 różnych adresów. Zdarza się faktycznie, że dwie (a nawet więcej) komisje mają siedzibę w tym samym budynku. Nie mając ani chęci ani czasu na dokładną inspekcję sprawdziłem jak wygląda rozkład siedzib/adresów względem liczby komisji:
perl chk_duplicated_coords.pl | sort -n ... 15 49.9062558 21.7658112 16 51.663189 16.5125886 18 51.2070067 16.1553231 20 49.9953359 21.3075494 28 50.5798603 21.6925451 40 52.6483303 19.0677357 50 54.3520252 18.6466384
Pierwsza kolumna to liczba komisji. Można przyjąć że jeżeli liczba komisji jest większa od 4 to doszło do błędnego geokodowania. Takich wątpliwych adresów jest:
perl chk_duplicated_coords.pl | awk '$1 > 4 {print $0}' | wc -l
142
Zostawiam ten problem na później przy czym z punktu widzenia wizualizacji za pomocą GFT, coś co ma identyczne współrzędne się nałoży na siebie, np. 50 komisji o współrzędnych 54.3520252/18.6466384 będzie pokazane na mapie jako jedna kropka (przy założeniu że zastosujemy kropkę do wizualizacji oczywiście). Żeby wszystkie komisje były widoczne (nawet te które mają prawidłowe ale identyczne współrzędne), to można zastosować losowe drganie (jitter). Tyle na razie.
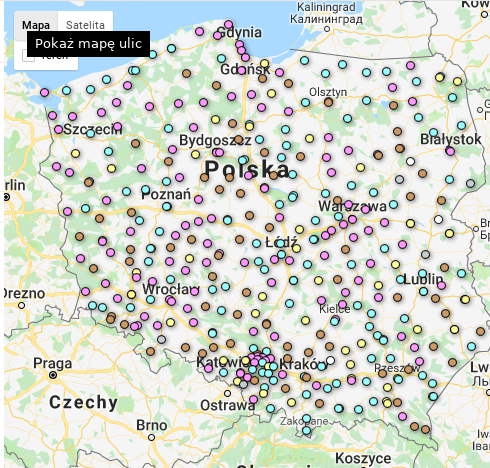
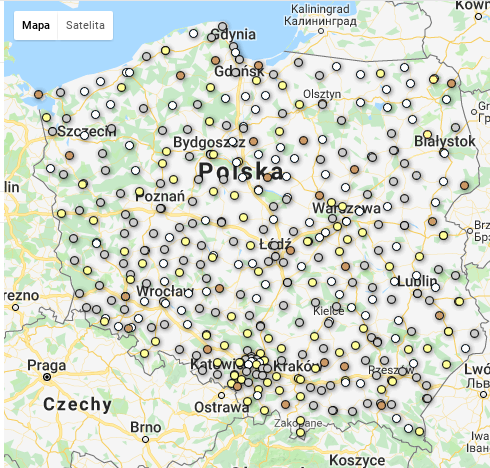
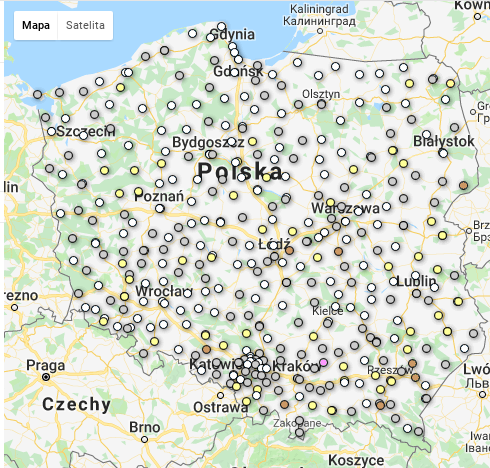
Plik powiaty_korelacje_pgnw_poparcie.csv zawiera m.in. obliczone w R współczynniki korelacji pomiędzy liczbą głosów nieważnych, a poparciem. Mam też plik zawierający obrysy powiatów i ich środki (teryt_powiaty_BB.csv). Na pierwszej mapie przedstawiono przeciętne wartości pgnw (odsetek głosów nieważnych). Czerwone i niebieskie kropki oznaczają wysokie wartości pgnw. Wyraźnie widać, że powiaty na zachodzie / północnym zachodzie mają wyższe wartości pgnw niż w pozostałej częsci kraju. Takiej przestrzennej zależności nie widać dla trzech pozostałych mapek, ilustrujących przeciętną wielkość współczynnika korelacji pomiędzy poparciem dla partii (PSL, PiS, PO) a odsetkiem głosów nieważnych. Wniosek: sympatycy wszystkich partii mylili się podobnie, a ich błąd był korzystny dla PSL.
Dane, skrypty i reszta wykresów są tutaj. Mapy GFT: poparcie/pgnw/powiaty oraz pgnw/obwody.
Brak komentarzy:
Prześlij komentarz